The procedure is similar to finding the shortest path through a network with no time-dependent travel cost (go there first).
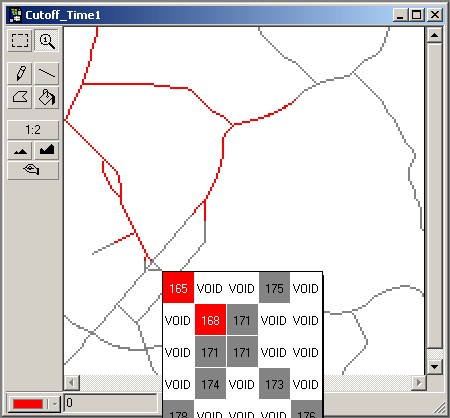
First calculate the path(s) from origin to the cutoff-point(s), where the new time interval starts. In other words spread until the available time in time interval 1, depending on your starting time, has been used up. From the cutoff-point(s) in time interval 1, calculate the shortest path(s) to the destination through time interval 2. The path with the lowest value is the sought path. Join the paths.
The cell value at the cutoff-point for time interval 1added to the cell values of the shortest path in time interval 2 is the total cost for the joined path.
If using 3 time intervals, repeat the procedure for time interval 1 in time interval 2. If using 4 time intervals, repeat the procedure for time interval 2 in time interval 3, and so forth.
SpreadFromStart_Time1= Spread start
To 600 (an arbitrarily chosen high value)
In costoftravel_time1
Outof direction
;
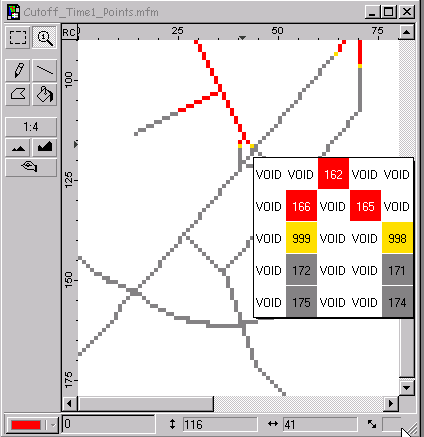
Cutoff_Time1 is derived by, in this case, assuming cutoff at 170. Alternatively, the value 170 can be inserted in the Spread operation as follows:
SpreadFromStart_Time1= Spread start
To 170
In costoftravel_time1
Outof direction
;
The cutoff-points are derived by manually assigning values to the cutoff cells and extracting them into separate layers.
Cutoff_Point1 = Recode SpreadFromStart_Time1
Assigning 1 To 999
Cutoff_Point2 = Recode SpreadFromStart_Time1
Assigning 1 To 998
Cutoff_Point3 = Recode SpreadFromStart_Time1
Assigning 1 To 997
Cutoff_Point4 = Recode SpreadFromStart_Time1
Assigning 1 To 996
;