Creating proximity surfaces from origin and destination and adding them yields the shortest path.
SpreadFromStart = Spread start
To 10000.00In costoftravel
Outof direction
;
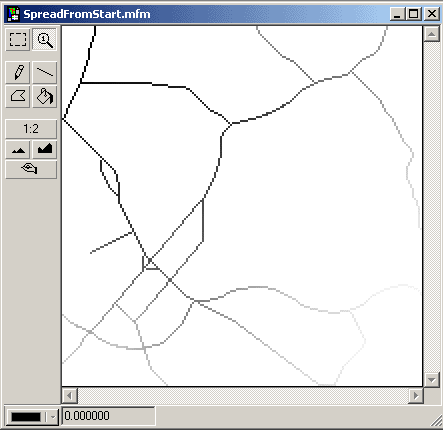
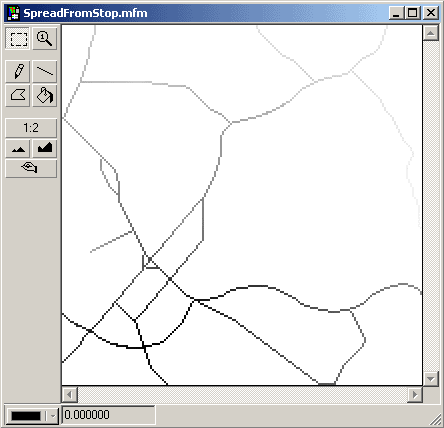
SpreadFromStop = Spread stop
To 10000.00
In costoftravel
Outof direction
;
ShortestPath_InNetwork = SpreadFromStart + SpreadFromStop
;
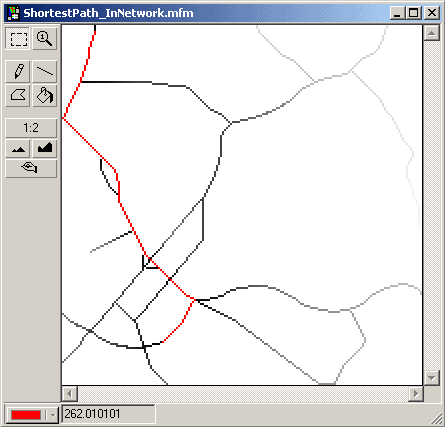
The shortest path is delineated by the cells with the lowest value(s). The value is the actual cost of using this path. Using the Legend function this path can be derived by changing the color of the cells with the lowest value until a continuous path from origin to detination can be seen.
…

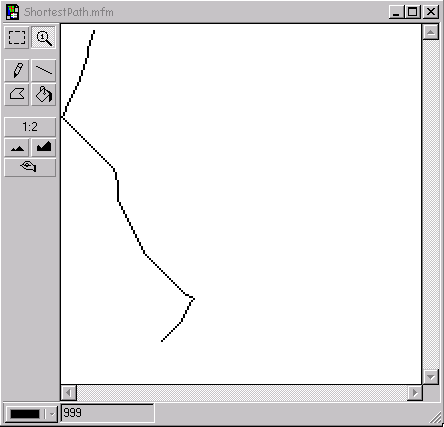
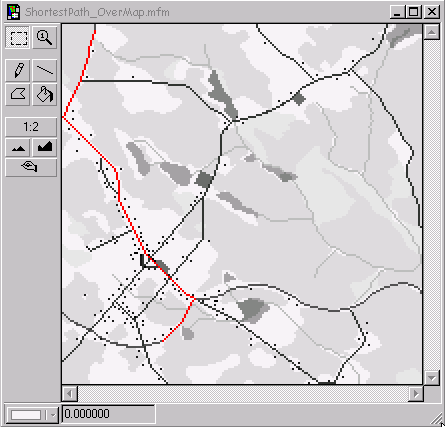
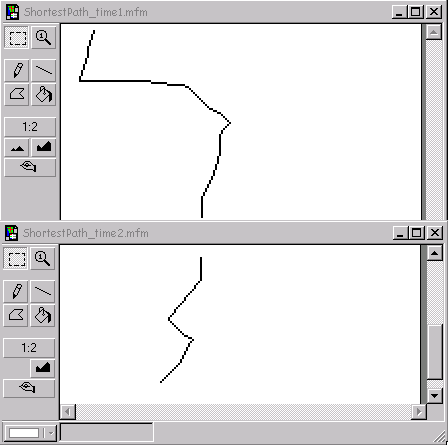


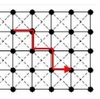 Locating a right-of-way for a linear facility such as a pipeline, a transmission line, a railway or a roadway can be a complex problem. Locating a corridor connecting an origin and a destination on a landscape is analogous to identifying a route that traverses a continuous landscape. Thus, corridor analysis is closely linked to shortest-path finding and network analysis in
Locating a right-of-way for a linear facility such as a pipeline, a transmission line, a railway or a roadway can be a complex problem. Locating a corridor connecting an origin and a destination on a landscape is analogous to identifying a route that traverses a continuous landscape. Thus, corridor analysis is closely linked to shortest-path finding and network analysis in